Craps
Craps is a dice game played in many casinos. You roll a pair of dice and if the sum is either 7 or 11, you win. If the sum is equals any of 2, 3 or 12, you lose. In any other case, the sum is logged. You then keep rolling the pair of dices until either the sum is 7 and you lose or the sum equals the logged sum and you win.
After calculating the theoretical probability of winning, the second section will run a simulation to inspect and visualize the chances of winning for a single player at a casino.
Theory
We calculate the probability of winning in two stages:
- Win in round 1 with rolling either a 7 or an 11
- Win in any other round with matching the sum rolled in the first round
The probability of winning in the first round, is then simply the probability of rolling either a 7 or an 11:
\[\begin{aligned} & P(7) = 6/36 \\ & P(11) = 2/36 \\ & P(7 \, or \, 11) = P(7) + P(11) = 8 / 36 \end{aligned}\]Any other number that does not lead to an instant lose, can be a potential win. As the player can keep rolling infinitely in the second stage, the probability should not be calculated on a round-by-round basis.
We rather will make use of the concept of conditional probability:
\[\begin{aligned} & P(A|B) = \frac{P(A \cap B)}{P(B)} \end{aligned}\]For example, a player rolled dices with a sum of 5 in the first round. The game will continue until the player rolls either a sum of 5 or 7. And the player wins when rolling a sum of 5.
Therefore the probability of winning is: “The probability of rolling a sum of 5 conditional on rolling a sum of 5 or 7”. The conditional probability is as follows:
\[\begin{aligned} & P(5\, | \, 5 \, or \, 7) = (4/36)/(10/36) = 2/5 \end{aligned}\]And the total probability:
\[\begin{aligned} & P(5) * P(5\, | \, 5 \, or \, 7) = 4/36 * 2/5 = 2/45 \end{aligned}\]For all sum of dices that do not end the game in the first round, the total probability of winning in any round after can be calculated as:
\[\begin{aligned} & P(4) * P(4\, | \, 4 \, or \, 7) = 3/36 * 1/3 = 1/36 \\ & P(5) * P(5\, | \, 5 \, or \, 7) = 4/36 * 2/5 = 2/45 \\ & P(6) * P(6\, | \, 6 \, or \, 7) = 5/36 * 5/11 = 25 / 396\\ & P(8) * P(8\, | \, 8 \, or \, 7) = 5/36 * 5/11 = 25 / 396\\ & P(9) * P(9\, | \, 9 \, or \, 7) = 4/36 * 2/5 = 2 / 45 \\ & P(10) * P(10\, | \, 10 \, or \, 7) = 3/36 * 1/3 = 1/36 \end{aligned}\]Which results in a total probability of winning of ~49%.
\[\begin{aligned} & 8/36 + 2*(1/36 + 2/45 + 25/396) = 244/495 = 0.4929293 \end{aligned}\]Simulation approach
The theoretical approach assumes the law of large numbers. Meaning, these probabilities are valid for long-run experiments. Which is the case for the casino-owner but not the individual players at the casino.
Meaning, the casino owner can rightly assume it will win 51% of the time and make a profit with offering the game of craps. An individual player cannot assume to play 100 rounds of craps and win 49% of the times.
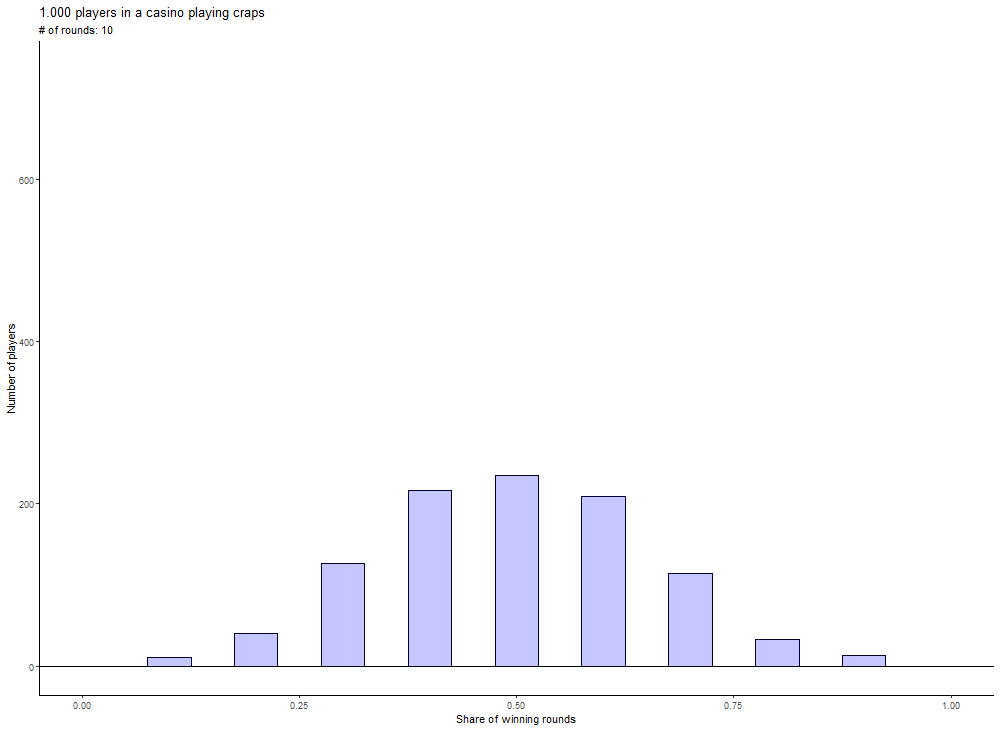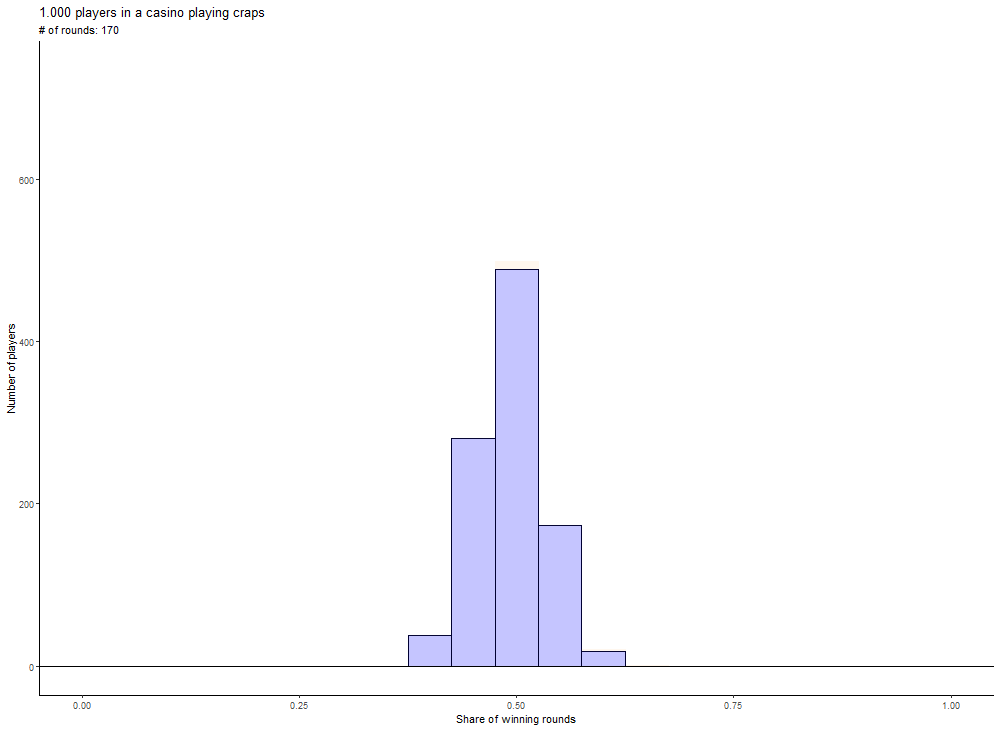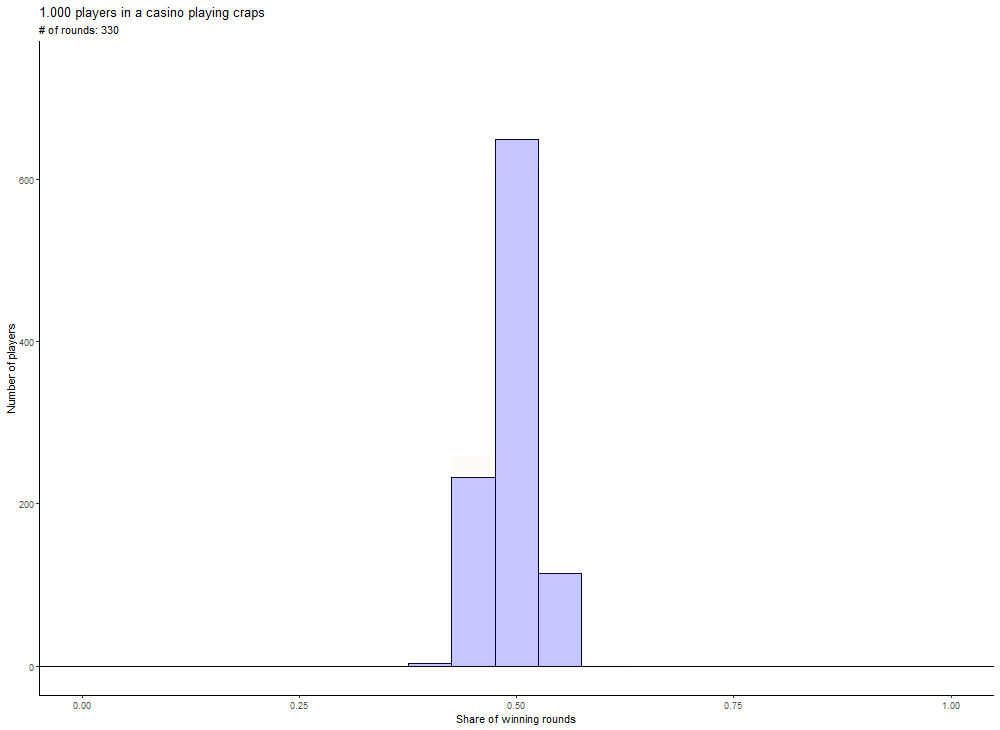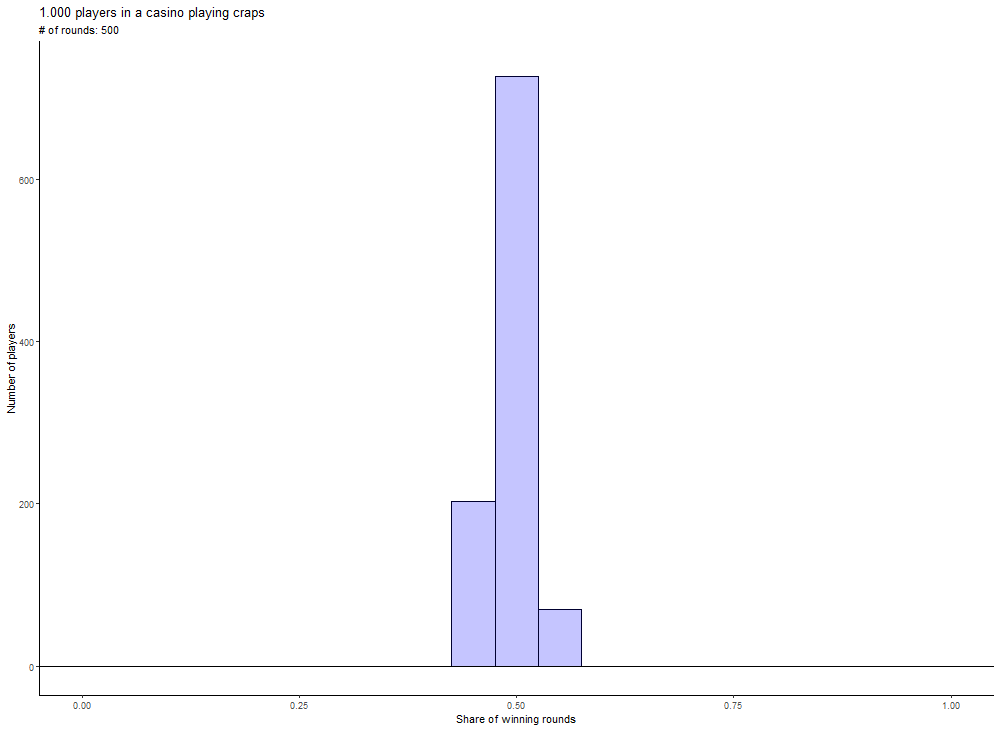
An intuitive approach to this problem is a simulation. Let us assume there are 1.000 people in a casino. And all of them play 10 rounds of craps. There can be some players who win all 10 rounds and some who will lose all of them. Now, if all players play 100, 250 or 500 rounds, there will be fewer and fewer players that might win all the rounds. And more players will win about 50% of the rounds played.
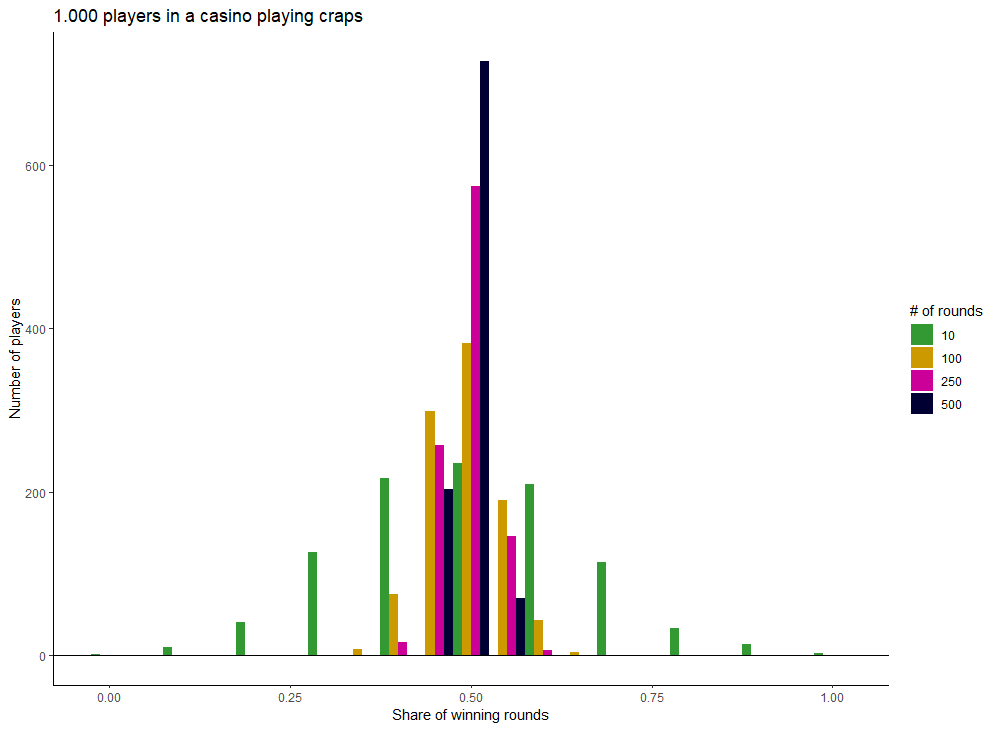
You can see that very observation also in the following animation, which displays the distribution for all number of rounds between 10 and 500, which are a multiple of 10.
Code
# Roll n dices
roll_dices <- function(n) {
sample(1:6, n, replace = T)
}
# Calculate second stage
points_game <- function(winning_sum) {
# First, we roll the dices again
roll <- roll_dices(2)
# Then we determine win / or loss
if (sum(roll) == winning_sum) {
return(1)
} else if (sum(roll) == 7) {
return(0)
} else {
# We can throw again.
points_game(winning_sum)
}
}
# --- simulate n players each playing x rounds
sim_players <- function(n_players = 1000, n_rounds = 100) {
set.seed(123456)
number_of_winning_rounds <-
lapply(1:n_players, function(n){
result_simu <-
lapply(1:n_rounds, function(x){
# First round
roll <- roll_dices(2)
result <-
if (sum(roll) == 7 | sum(roll) == 11) {
# Win
1
} else if (sum(roll) == 2 | sum(roll) == 3 | sum(roll) == 12) {
# Lose
0
} else {
# Point
points_game(sum(roll))
}
result
})
result_simu <- unlist(result_simu)
mean(result_simu)
})
unlist(number_of_winning_rounds)
}
# Check if simulated probability roughly equals theoretical probability
sim_players(n_players = 1, n_rounds = 10000)
# Assume 1.000 players in a casino.
# Simulate that each player plays: 10, 100, 250, 500 rounds
library(dplyr)
library(tidyr)
library(ggplot2)
df_simu <- data.frame(n = 1:1000)
df_simu <-
df_simu %>%
mutate(
r_10 = sim_players(n_rounds = 10),
r_100 = sim_players(n_rounds = 100),
r_250 = sim_players(n_rounds = 250),
r_500 = sim_players(n_rounds = 500),
)
df_simu_long <- df_simu %>% pivot_longer(cols = -c(n))
ggplot(df_simu_long, aes(x = value, fill = name)) +
geom_histogram(binwidth = 0.05, position = position_dodge()) +
scale_fill_manual(values =
list("r_10" = "#339933",
"r_100" = "#CC9900",
"r_250" = "#CC0099",
"r_500" = "#000032"
),
labels = c("10", "100", "250", "500")) +
labs(title="1.000 players in a casino playing craps",x="Share of winning rounds", y = "Number of players")+
guides(fill = guide_legend(title = "# of rounds")) +
geom_hline(yintercept = 0) +
theme_classic()
# And now, let's animate this!
library(gganimate)
df_simu <- data.frame(n = 1:1000)
for (n_r in seq(10, 500, 10)) {
df_simu <- bind_cols(df_simu, sim_players(n_rounds = n_r))
}
df_simu <- df_simu %>% setNames(c("n", paste0("r_", seq(10, 500, 10))))
df_simu_long <- df_simu %>% pivot_longer(cols = -c(n))
df_simu_long %>%
mutate(name = gsub("r_", "", name)) %>%
mutate(name = as.integer(name)) %>%
ggplot(aes(x = value)) +
geom_histogram(binwidth = 0.05, fill = "#C5C5FF", color = "#000032") +
xlim(0, 1) +
labs(
title = "1.000 players in a casino playing craps",
subtitle = '# of rounds: {closest_state}',
x = "Share of winning rounds",
y = "Number of players") +
geom_hline(yintercept = 0) +
theme_classic() +
transition_states(name) +
ease_aes('linear')