A Triangle of Pool Balls
In a game of pool, there is a set of 15 balls with values 1 to 15 that are arranged in a triangle at the beginning of the game. Is there a way to arrange the balls in way, that each number below a pair of balls equals that positive difference of that pair?
(Source: “The colossal book of short puzzles and problems” by Martin Gardener)
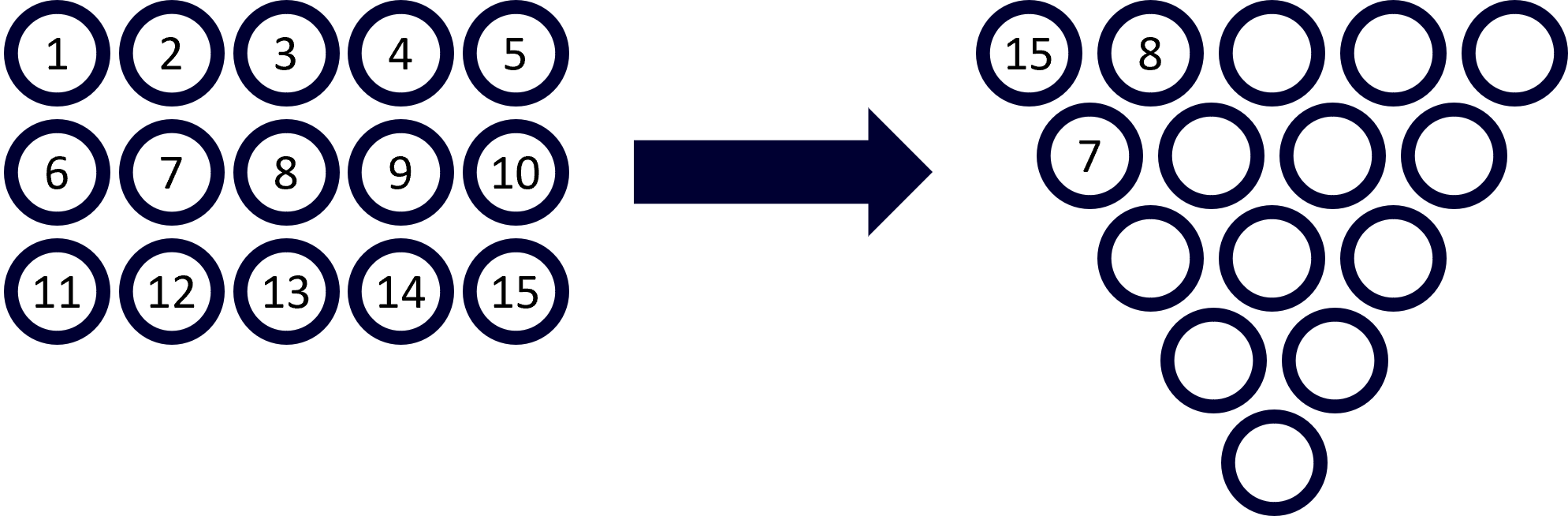
The order of balls in the first rows determines the positions of balls in all other rows. There are 15 * 14 * 13 * 12 * 11 = 360,360 possible arrangements for the first row.
By defintion of the problem, the ball with the number 15 needs to be in the first row. This reduces the number of possible possibilities to 14 * 13 * 12 * 11 * 5 = 120,120.
To solve this problem by hand, further logics can be applied to reduce the number of possibilities. For example, the number 14 cannot be in row 1 if both 15 and 1 are there.
Algortihm
Define m_1 as a matrix of all possible combinations for the first row.
For all rows in m_1:
- Define a matrix m with 5 rows and columns
- Fill the first rows with current values from m_1
- Calculate rows 2 to 5 in the upper triangle
- Solution found if there are no 0 or duplicate values in the upper triangle
(See the code at the end of the post)
Solution
This problem can yield only two solutions which are reflections of one another.

Generalization
The number of possible combinations for the first row increases very quickly.
| # in 1st row | # Balls | Comb in 1st row | Solutions | Calculation Time (in sec) |
|---|---|---|---|---|
| 2 | 3 | 2 * 2 = 4 | 4 | 0.03 |
| 3 | 6 | 5 * 4 * 3 = 60 | 8 | 0.03 |
| 4 | 10 | 9 * 8 * 7 * 4 = 2,016 | 8 | 0.05 |
| 5 | 15 | 14 * 13 * 12 * 11 * 5 = 120,120 | 2 | 1.29 |
| 6 | 21 | 20 * 19 * 18 * 17 * 16 * 6 = 11,162,880 | 0 | 122.4 |
| 7 | 28 | 27 * 26 * 25 * 24 * 23 * 22 * 7 = 1,491,890,400 | 0 | ??? |
Unfortunately, even the more efficent code cannot calculate cases beyond 6 in a reasonable amount of time. But, according to the book reference by Thomas Gardener, there are no solutions anyways.
Code
# Standard case ------------------------------------------------------------------
# Calculate total number of balls depending on length of first row.
n_1 = 5
n_total = sum(1:n_1)
# Matrix of possible combinations for first row
m_1 = expand.grid(rep(list(1:n_total), n_1))
m_1 = as.matrix(m_1)
# Drop rows with duplicates
m_1 = m_1[apply(m_1, 1, function(x) length(unique(x))) == n_1,]
# Drop rows without the largest number
m_1 = m_1[apply(m_1, 1, max) == n_total,]
# Try all combinations; break when solution found
for (r in 1:nrow(m_1)) {
# Initialize matrix
m <- matrix(0, nrow = n_1, ncol = n_1)
# Fill first row of matrix
m[1,] <- m_1[r,]
# Calculate all subsequent rows
for (i in 2:n_1) {
for (j in i:n_1) {
m[i,j] <- abs(m[i-1, j-1] - m[i-1, j])
}
}
# Extract upper triangular matrix
m_u = m[upper.tri(m, diag = T)]
# Check if there are any 0
if (sum(m_u == 0) == 0) {
if (length(unique(m_u)) == length(m_u)) {
break
}
}
}
print(m)
# General case ---------------------------------------------------------------
# Calculate total number of balls depending on length of first row.
n_1 = 6
n_total = sum(1:n_1)
# Remove duplicates on efficient subsets:
# The largest number n_total needs to be in the first row
# There are n_1 possible positions which define the subsets
m_1 <-
lapply(1:n_1, function(i) {
# Create matrix for current position of n_total
l_i = rep(list(1:(n_total - 1)), n_1)
l_i[i] = n_total
m_i = expand.grid(l_i)
m_i = as.matrix(m_i)
# Drop duplicates
cols <- combn(1:n_1, 2)
for (c in 1:ncol(cols)) {
c_1 = cols[,c][1]
c_2 = cols[,c][2]
m_i = m_i[m_i[,c_1] != m_i[,c_2],]
}
m_i
})
m_1 = do.call("rbind", m_1)
l_solutions <- list()
# Try all combinations; find all solutions
for (r in 1:nrow(m_1)) {
# Initialize matrix
m <- matrix(0, nrow = n_1, ncol = n_1)
# Fill first row of matrix
m[1,] <- m_1[r,]
# Calculate all subsequent rows
for (i in 2:n_1) {
for (j in i:n_1) {
m[i,j] <- abs(m[i-1, j-1] - m[i-1, j])
}
}
# Extract upper triangular matrix
m_u = m[upper.tri(m, diag = T)]
# Check if there are any 0
if (sum(m_u == 0) == 0) {
if (length(unique(m_u)) == length(m_u)) {
l_solutions[[length(l_solutions) + 1]] <- m
}
}
}
print(length(l_solutions))